Storing and retrieving data in a non-volatile memory is the primary function of any database. Obviously we have to make the retrieving decently fast, and given that disk speed is said to be 10000 times slower then memory, storing them efficiently even on disk is important.

B-Plus Tree Link to heading

Storing them efficiently on disk is where the B-Plus tree starts coming in handy. Although most modern DB engines use a lot of optimizations on top of these, getting a hands-on idea of implementation on a weekend felt like a good idea.

So this what we will be doing, our basic tree class will be exposing a limited functionality (only insert and getto be specific) as shown below

public interface Tree<T,V> {
    String getName();
    boolean insert(T key,V value);
    V get(T key);
    void printTree();
}

First up, we are going to develop an intuition of how a B-Plus tree is implemented in memory and then extend that.

Revisiting an Undergraduate Course Link to heading

Let’s get a quick revision of a Binary Search Tree (BST). (Obviously, you do not have to know all the nitty-gritties), but the only important thing is each node has a key, and any node on the left side of this node has a key smaller than the current node’s key, and a node on the right subtree has a key bigger than the current node.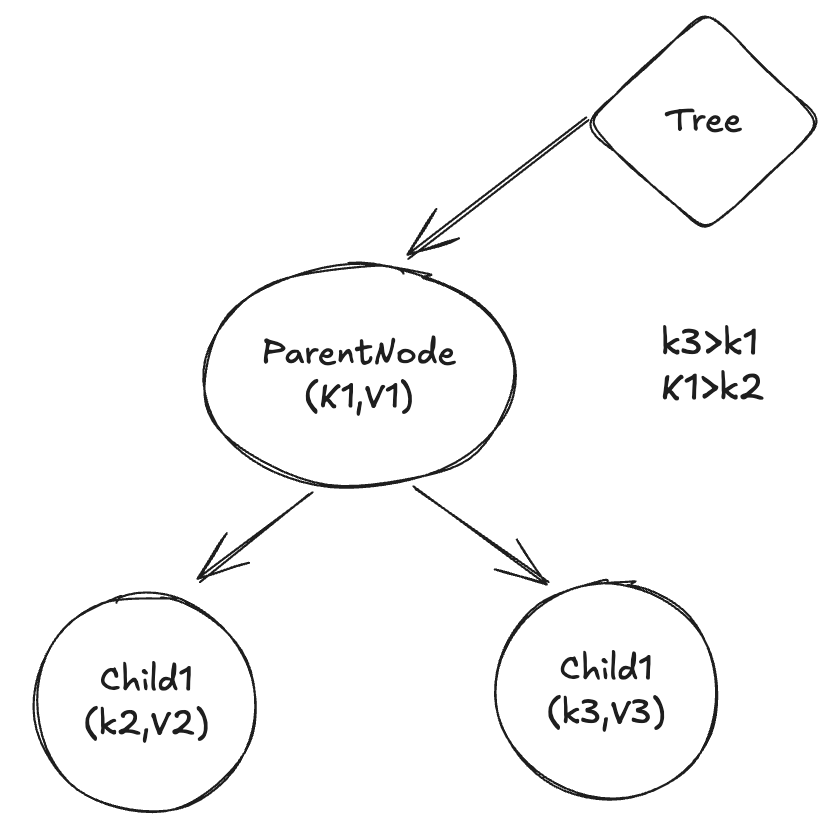

You can use this property to either move to left child or to the right child of a given node based on the requirement. So in one step, you are essentially removing half of all the keys in search space and continuing this until you get a desired state. Lets say that we have $N$ distinct keys This helps us to insert and retrieve any new node in $\log(N)$ iterations (which translataed to about $30$ iteration for even $10^9$ distinct keys) on an average. If you are not too comfortable with these ideas, I would recommend you to practice by implementing them this leetcode problem

The downside of this is, there is a way to get a skewed Binary Search Tree, where we can no longer discard half of the search space in one step. a GET operation can now be O(N) and insertion is also O(N) which would is too slow even for an in memory structure.

To overcome this, we will need to add some kind of balancing after each insertion operation¹. There are several algorithms for this, such as AVL Tree, Red Black Tree but we are going to use B+ tree as a self balancing tree, since once we have that down, implementing that for disk will require just a couple of tweaks

B+ Tree as self balancing tree Link to heading

Lets follow a simple strategy to balance our search tree. First instead of storing 1 key per node, I am going to store 2 keys per nodes $(K0 < K1)$ and instead of 2 child per node, I am keeping 3 child per node $(C_0,C_1,C_2)$. Obviously we can update properties of this modified tree as well

• For all keys in subtree of $C_0$ will have $K_{c_0} < K_0$
• For all keys in subtree of $C_1$ will have $K_0 < K_{c_1} < K_1$
• For all keys in subtree of $C_2$ will have $K_{c_2} > K_1$

How does insertion look like in this tree?

• Find the leaf node, below which the insertion have to be done.
• Scenario 1 - We add a key, on a node which has only one key - No change needed as tree structure is the same.
• Scenario 2 - We add a key, on a node which has two keys - We let this node overload and push the middle node to its parent, while splitting this node.

You will observe that with a jump added into the mix and adding nodes to a leaf node, you always ensure that the search space is uniformly distributed². A surprising completly unrelated thing is this is the exact intuition for implementing a red black tree on your own as well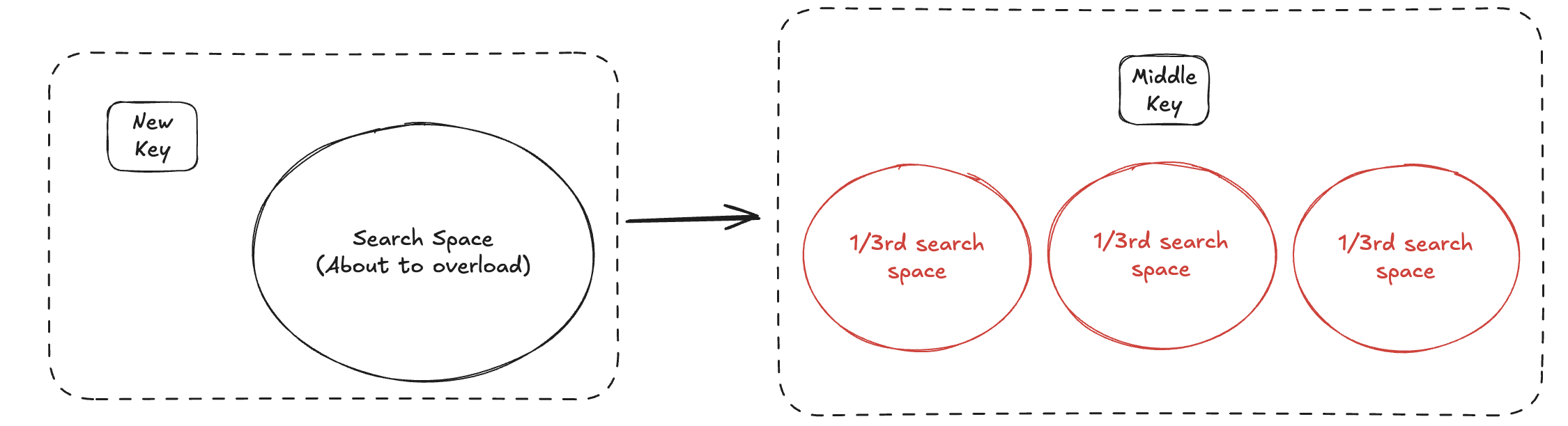

Now we can also extend our existing tree structure to have $N$ nodes and $N + 1$ children, and for pushing up, we can use the middle most key of the node.

Is this B+ tree? Not really, we did not talk about how we are going to store the value. This is where B Trees and B+ Trees differ. While in a B tree we store a value pointer at each node along with the key, in a B+ tree we store the keys only in nodes and store the value pointer at the leaf. So there is key duplication at one leaf node and at some other node.

Why do we do this? It makes range operation quicker as once we have reached a leaf node, we can retrieve all the element onwards traversing over the leaf nodes and going to other leaf nodes using next and prev pointers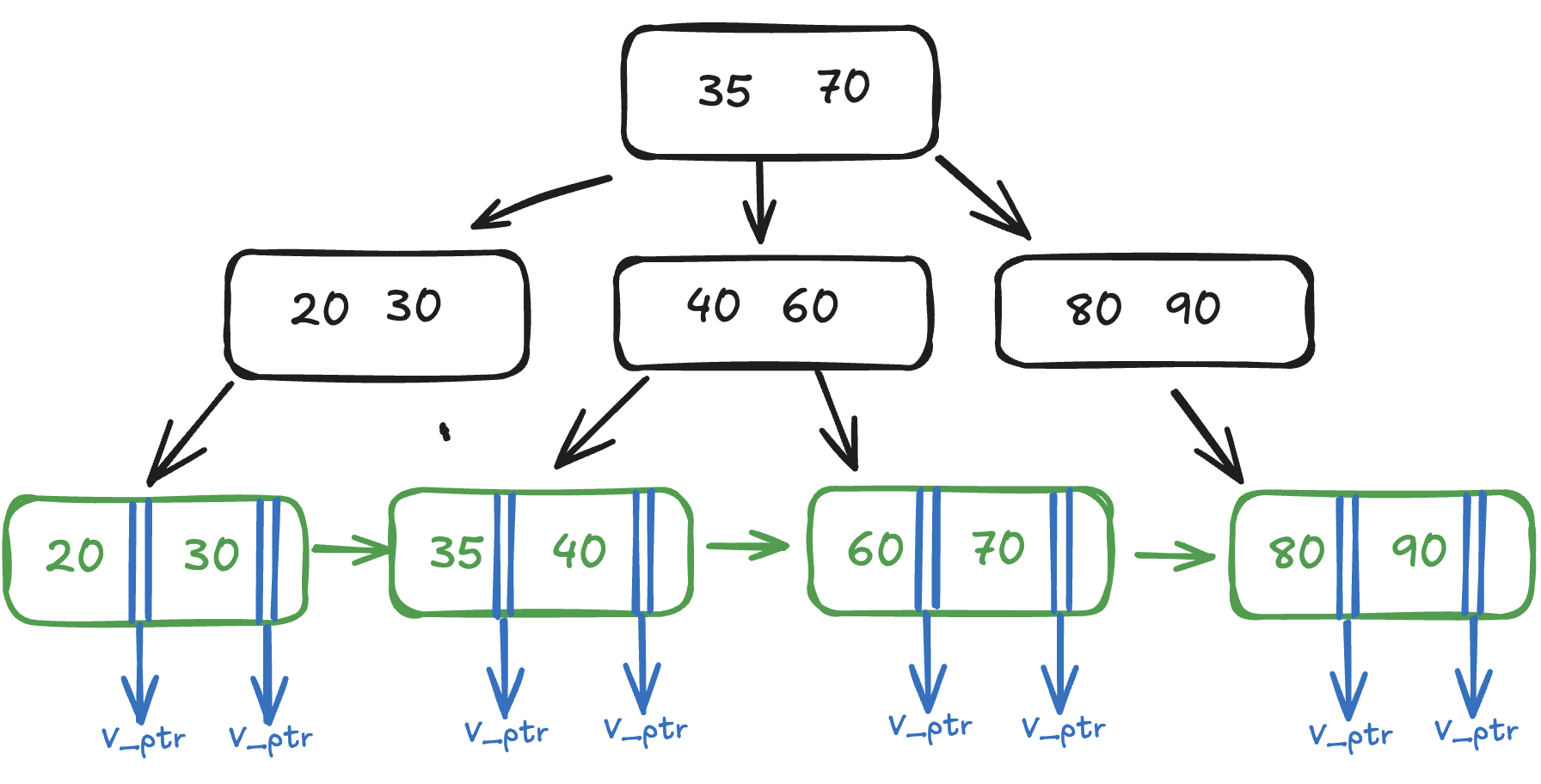

If you want to get a hang of B+ tree structure with your examples, checkout this amazing visualizer

In Memory B+ tree implementation Link to heading

We have the basics down, now its time to go about implementing. And for in memory B tree, its just really annoying binary search tree but with few more classes and one extra function - split(Node) which is the heart of B plus tree to split the node and return the middle most key. A very rough idea for implementation this for in memory is as follows:

class Node<K,V> {
    boolean leaf;
    V value[N]
    K keys[N]
    Node childNode[N + 1]
    Node nxt
    Node prev
}

func insert(K key,V value,Node node){
    if(node.isLeaf()){
        node.add(key,value)
        return split(node)
    } else{
        position = node.findPositionForKey(key)
        newNode,newMiddleKey = node.add(key,value,node.getChild(postition))
        if(newNode == null){
            return null
        }
        node.add(newNode,newMiddleKey)
        return split(node)
    }
}
func split(Node node){
    if(!node.isfull()){
        return null
    }
    middleKey = node.keys[key.size()/2]
    nodeA = node.key{0,key.size()/2}
    nodeB = null
    if(node.isLeaf()){
        nodeB = node.key{key.size()/2,key.size()}
    } else{
        nodeB = node.key{key.size()/2 + 1,key.size()}
    }
    node = nodeA
    return (nodeB,middleKey)
}

This is an extremely simplified code, but if you are looking to get an hands-on example, do find the code here. And with this we have a self balancing tree. But how do databases actually implement this?

Storing B+ tree in non-volatile Link to heading

OS retrieves data from disk to in memory using page. Each page is essentially is contiguous segment in disk that is loaded in memory. Lets use a file (say database.txt) to store our data.

The bottle neck is retrieving this page from file (Disk IO). So we try to pack as much information information into one page as possible, so that we do less D isk-IO. In case of B+ tree, a node is essentially 1 page. We try to pack as many keys inside 1 page, but at the same time, keep track of child nodes (other pages) as well.

So our node will be looking somewhat like this, keep in mind that instead of restricting the key of fixed size, we make it variable, since page size can be variable in different systems. And we want to utilize as much page size as possible.

Node {
    Integer CurrentNodeOffset
    boolean leaf;
    V value[]
    K keys[]
    Integer childNodeOffset[]
    Integer nxtNodeOffset
    Node prevNodeOffset 
}

How to store 1 node in disk?, we store them in byte format, which is more commonly knowns as serialization. Most languages provide us with a way to serialize primitive data types, but in this case, we also have user defined types (K,V) in the node. Since this is user defined, ideally I would also want to make the serializing user-defined as well and thats where the interface of serializing should be made, which shifts freedom to user to have their own serializer

interface Serializer<T> {
    void serialize(inputStream, T key);
    T deserialize(inputStream);
}

So we have the structure to store node , we will also need an extra disk manager, whose job would be to

• Retrieve a file and get the root node offset for B+ tree
• Convert a given offset to an actual in-memory node
• Given an in memory node, flush this to the file IO.

And hence the low level design would be looking something like this.

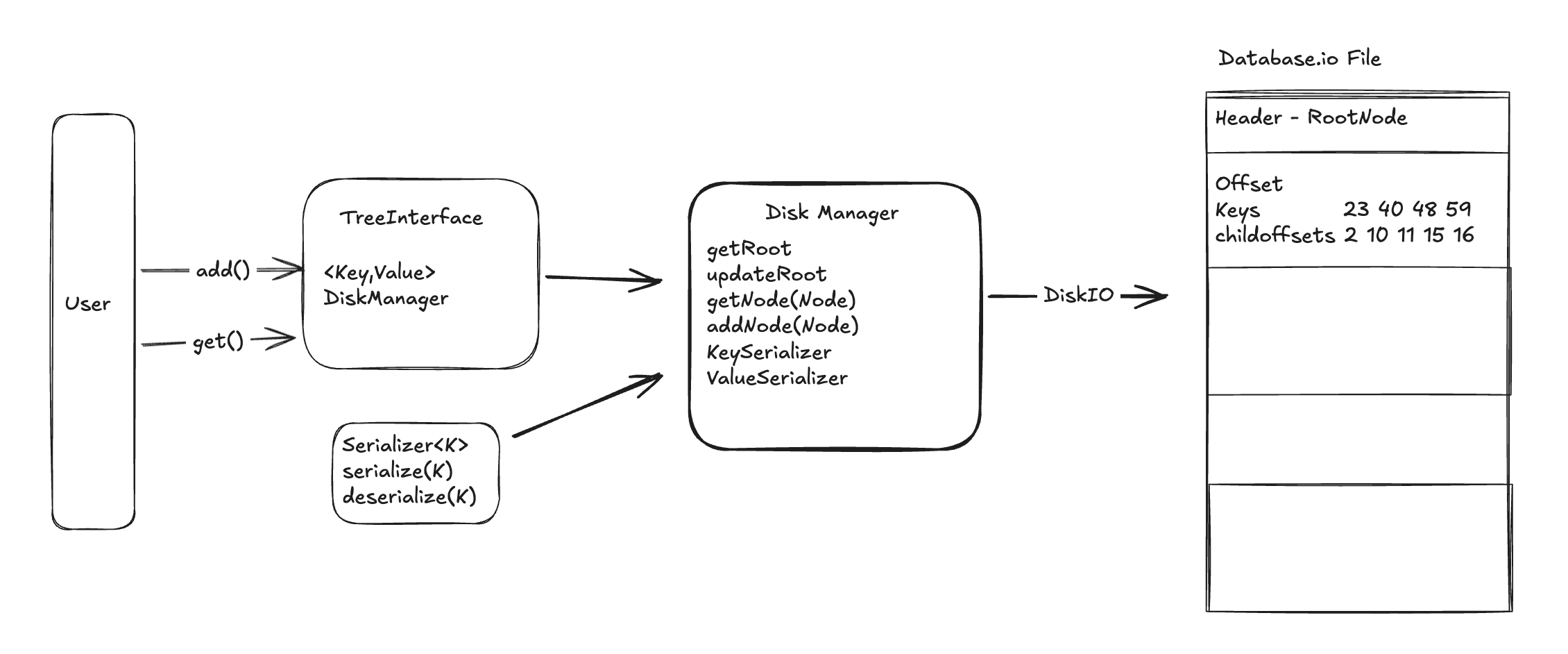
You can find the full code for disk implementation of B+ tree here

Lets do some estimates to get an idea how optimized search looks like in B+ tree. On an average, a page is of $16Kb$ size. So thats about $1000$ keys. I am going to take a much lower value, $500$ to account for maybe storing strings as value as well.

• So root node have $500$ keys and it can have 500 childs
• Each $500$ child have $500$ additional keys, so that $500 * 500 = 2.5 * 10^5$
• Add in one more layer and we have $2.5 * 10^5 * 500 = 1.25 * 10^8$
• One more layer - $1.25 * 10^8 * 500 = 6.25 * 10^{10}$!!! So in just 4 layers, we are storing more than ten billion keys. And in only 4 Disk-IO, we can retrieve the key that the user wants.

Obvoiusly we have super quick reads, but an insert operation will require us to do 4 Disk-IO as well, and thats where LSM trees comes to play.

I will e implementing an LSM tree as well, but for now, lets end this blog here as thats an entirely different topic. So until next time, happy implementing!

Footnotes Link to heading